Co-Ordinate
Geometry
A quote from Anatole France:
“The whole art of teaching is only the art of
awakening the natural curiosity of young minds for the purpose of satisfying it
afterwards.”
Co-ordinate Geometry
The founder (Father of Co-ordinate geometry) was Rene Descartes, his Latin name was Rene Cartesian, so term ‘Cartesian Plane ‘, cartesian co-ordinate System established/ obtained, from his name. It is also known as analytic geometry.
Rene Descartes (March 31, 1596, -February 11, 1650)
We know geometry is a branch of mathematics where we study the size, shape, 2 dimensional figures, Solids. The topic, Co-ordinate Geometry is an interesting concept of mathematics. It describes the link between geometry and algebra through graphs involving curves and lines. It is nothing but geometric aspects in algebra. It is a part of study of geometry using a co-ordinate system., where we are able to locate a point in a given (2D/ 3D) plane.
The earth has imaginary lines, a co-ordinate system known as longitudes
and latitudes. Location of a point on earth, one can easily find out rather we
can trace out. For that we have to have a reference point. Whenever we wish to
find out the distance between two places, on road, we type the names of the
places say A to reach the place B; so, distance is given with respect to a
reference point. That reference point we
take it as origin. For convenient, we do draw 2 perpendicular lines
(horizontal, vertical). They do intersect at a point, is the point of origin,
the reference point. The horizontal line and vertical line we call them
co-ordinate axes. The horizontal line we call as X - axis, the vertical line we
call Y – axis. We do call them as co-ordinate axes. It divides the plane into 4
quadrants, counted in the anti-clockwise direction.as I, II, III, IV as four
quadrants. To right and above origin(O) positive values, to the left of origin
and down below(O) are negative values.
Application: Definitely its
wide applications are there, namely, in 3-D geometry, equations, calculus,
complex numbers, vectors. Very much used in physics, aviation, space science,
rocketry, space flight. Its application is being used in ‘digital equipments
‘(mobile phones, computers), to locate a point in maps. GPS, so on. The
students who go for engineering course, (study) very helpful for them.
Let me proceed further with the introduction, preliminary
concepts, on this topic.
In a plane the points are located in the ordered pairs
(x, y). The values of the ordered pair are known as co-ordinates of the point.
The first value of the point is called as Abscissa, second value is
called as Ordinate. I have already mentioned about 4 quadrants. I
quadrant (+ve, +ve), II Quadrant (-ve, + ve)
III
Quadrant (- ve, - ve), IV quadrant (+ ve, - ve). It is to be known that, in the
ordered pair, the first point say x is to be taken on X axis, the second point say
y is to be taken on Y axis, The order is very important so to say in location
of a point. The pair (3, 4) denotes a point while (4,3) denotes some other
point. One has to take more care in plotting points where does the point lie I /
II /III / Iv.
Note:
Co-ordinate of origin is (0, 0), the reference point. With reference to the Origin,
we locate the co-ordinate points.
Section
Formula: Given a line segment. If a
point say P divides the line segment internally, in the ratio m:n,
to find the coordinates of the point P.
Let the given line segment be AB with
coordinates A be (x1, y1), B be (x2, y2), P be (x, y). In this case also, we use the properties of Similar Triangles. If
two triangles are similar, the corresponding sides are proportional. Using this
principle, the coordinates of P
x = (mx2
+ nx1) / m+ n and y = (my2
+ n y1)/ m + n.
{(kx2
+ x1) / k +1, (ky2+ y1) / k +1 } ., We can
deduce to find the mid-point of a line segment. ie to say, if P divides the
line segment in the same ratio,
m1
=m2. In that case Coordinates of P ( x1 + x2 )/ 2 , ( y1 + y 2)
/ 2.
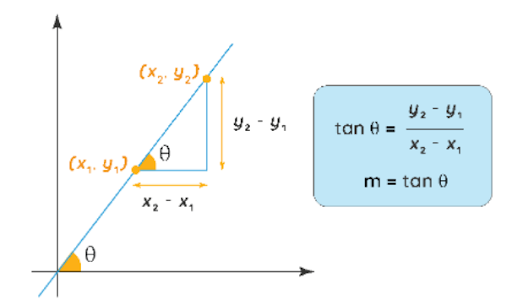
III Slope of a Line : This part of Co-ordinate geometry is linked with Trigonometry ratios. The slope of a line with respect to another line is the angle between the two lines. We do know the ratio
tan q = Perpendicular/ Base .
Given the line segment AB, with A (x1, y1), B (x2, y2) is y2 –y1 / x2 – x1 .
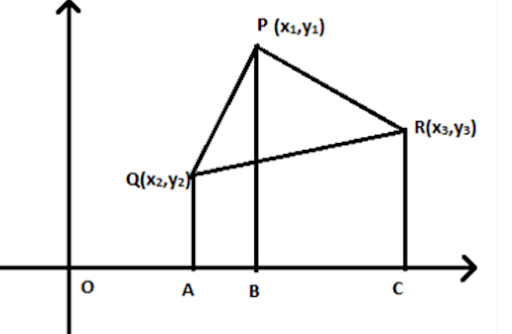
Area of Triangle :- In co-ordinate geometry, the area of triangle whose vertices are given can be calculated easily using the given formula.
"Enthusiasm is
the mother of effort, and without it nothing great was ever achieved."
-------- Ralph waldo Emerson.
Problems using distance formula:
1.The triangle is formed by the points P (2,7), Q (4, -1), R (-2,6). What kind of triangle, is it?
Solution:-
PQ = Ö (4-2) ^2 + (-1 -7) ^2 =Ö 4 + 64 = Ö 68.
QR = Ö( -2-4) ^2 + (6+1) ^2 = Ö 36 + 49 = Ö85
RP = Ö( -2-2) ^2 + (6-7) ^2 =Ö16+ 1 = Ö17.
By finding the length of the sides,
we come to the conclusion;
the triangle is right angled triangle since
PQ^2 +RP^2 = QR^2 using Pythagoras theorem.
2.The points P (a, b+ c), Q (b, c +a), R (c, a +b) are such that PQ = QR, Prove that a, b and c are in A P.
Solution:- Let us use the distance formula:
PQ^2 = (b-a) ^2+(c +a
-b-- c) ^2 = b^2+a^2 -2ab +a^2 +b^2-2ab) =2(a-- b) ^2
QR^2 = (c-b) ^2+(a+ b -c -a) ^2=
c^2+b^2-2bc+b^2+c^2-2bc) = 2 (b--c) ^2
i.e. since given PQ = QR, 2(a- b) ^2 = 2 (b - c) ^2
we
get a -b = b -c (by taking the square root)
b = (a+ c) / 2, which shows that a, b, and
c are in AP.
3.Prove that the given points are collinear. P (0,4), Q (1,3), R (2,2).
Solution:- If PQ +QR = PR, we can say P, Q, R are
collinear. Other way if area of triangle is zero.
(PQ)^2 = (1 –
0) ^2 + (3 -4) ^2, (QR)^2 = (2 -1) ^2 + (2 – 3) ^2,
PR ^2 = (2 – 0) ^2 + (2 -4) ^2, PQ = Ö 2, QR = Ö2. PR = 2Ö2.
Hence we can say P, Q, R are
collinear.
4. Find the
of x, for which the distance between A (x, -3), B (10, -9) is 10 units.
Solution : Using the distance formula
AB = Ö (10 -x) ^2) + ( -9 +3) ^2 = 10
Squaring both sides, (10 -x)^2) + ( -9 +3) ^2 = 100,
so, 100+ x^2 -20x +36 = 100
We get Q equation x^2 – 20x +36 = 0,
solving we get ,
(x-2) (x -18) = 0
Therefore, x = 2 , 18 are two solutions
5.Find a relation between x and y such that the point P (x, y) is equidistant from A (2,6), B (9, 7).
Solution : Let P (x, y) be equidistant from A, B, then AP = BP,
So, (AP)^2 = (BP)^2
(2 -x) ^2 + (6 -y) ^2 = (9 -x) ^2 + (7
-Y) ^2
Expanding the terms, we get
4 +x^2 – 4 x +36 + y^2 – 12y = 81 +
x^2 -18x +49 + y^2 – 14 y,
After simplification, the required
equation is 14 x + 2 y –90 = 0.
Section Formula
6.Find the ratio in which the line joining the points A (2,3) and B (5, -1) is divided by X axis.
Solution:- Let the ratio be k:1, by using the formula, the coordinates of the point which divide AB, in the ratio k:1 are
{ 5k+2/ k +1, -k+3 / k +1} ,since the dividing point is on the X axis, hence y co-ordinate = 07. Find the ratio in which the line segment joining A ( -3,10) and B (6, -8) is divided by the point ( -1,6).
Ans: Let P(-1,6) divide the line segment AB internally in the ratio l: m
Using the section formula (-1,6) ={ 6l – 3m/l+ m, -8l +10m / l+ m }
-1 = 6l – 3m/ l+ m, solving 7 l = 2 m, so
l/m = 2 /7,
Hence the ratio is 2: 7.
Area of
Triangle:
8. Find the area of triangle whose vertices are A (-6, 0), B (1,1) and C (0,2)
Solution:-
We know area of triangle = 1/2 { x1 (y2 – y3) + x2(y3
-y1) + x3 (y1 – y2) }
= 1/2 { -6 (1 - 2) + 1 (2 –0) + 0 (0 -1) }
= 1 / 2 {
-6 x -1 + 2) } = 4 sq units.
9.Find the area of triangle formed by joining the mid points of the sides of triangle whose vertices are A (0, -1), B (2, 1), C (0, 3).
Solution : Let D, E, F be the midpoints of AB, BC, CA.
D{ ( 0+2)/ 2, ( -1+1)/ 2} ; E{ ( 2+0 /2, (1+3)/2} ; F { (0 +0)/ 2, (3 -1) /2 }
ie D (1,0),
E (1,2) F (0,1).
Now,
ar (DEF) = 1/2{ 1 (2 -1) + 1(1 -0) +0 (0 -2) }
= (1/2) x 2 = 1 Sq units
10. Find the length of the altitude from A of triangle ABC. Given A (-3,0), B (4, -1), C (5,2) are the vertices of triangle.
Solution:-
BC= Ö10, (using distance formula)
Let us
find the area of triangle.
Area = 1/ 2 { -3( -1 -2) +4 (2-0) +5 (0 +1) } = 1/2 (9 + 8 + 5) = (1/2) x 22 = 11 Sq. unit
We know Area of a triangle = 1/2 x Base x Height
11= 1 /2 x BC x AD,
Hence length of altitude AD = 22 / Ö 10. is the answer.
11. Find the centroid of triangle ABC, Given the vertices are A (2,3), B (3,5), C (7, 7).
By using the formula, if G (x,y) denotes
centroid.
Solution:-
x = (2+3+7) / 3, so x = 4
y = (3+5+7)/ 3, i.e. y = 5
Hence G (x,y) = G (4,5).
K . Bhanumoorthy