Numbers Bearing the Names of Mathematicians
Were it not for number and its nature,
nothing that exists would be clear to anybody either in itself or in relation
to other things. You can observe the Power of numbers exercising itself not
only in the affairs of the demons and gods but in all the acts and thought of
men, in all handicraft and music.
Everybody loves to play with numbers. Have
you played with numbers? While playing snakes and ladders you certainly play
with numbers. There are several mathematicians who got fascinated with the
charms of numbers and this section of chapter deals only with those numbers
which has been named after its discoverer. These numbers have special features
and they are special because they bear the name of mathematicians. For the convenient
of the readers a brief Bio-Data has been provided here so that they can get the
right information without much effort.
1. Ramanujan Number---- 1729
is called the Ramanujan Number. This is the least number which can be easily
expressed as the sum of the cubes of two numbers in different ways. It can be
written as 103+93 and 123+13. This
was in fact the number of a taxi Prof Hardy had hired when he came to see ailing
Ramanujan in the hospital. When Prof Hardy asked Ramanujan that the taxi he had
hired had a boring number; Ramanujan instantly said that this is the smallest
number which can be expressed as the sum of cubes of two numbers in two
different ways.
|
2. Euler Number:-This is the smallest number which can be
expressed as the sum of two fourth power in two different ways. This special
number was presented by great mathematical genius Leonhard Euler (1707-1783).
635318657=
1334 + 1344 = 594 + 1584
Leonahrd
Euler was born on 15 April 1707 in Basel in Switzerland. He was an exceptionally
brilliant mathematician. He completed his Master’s degree in Philosophy in
1723. He served as a medical Lieutenant
in the Russian Navy from 1727 to 1730. In 1730 he became a Professor of Physics
at the Academy and left the Russian Navy Port job. Tragically when he was at
the age of 28 he became completely blind but this true mathematics lover never
took a rest. While blind he published more than 400 mathematical papers, most
of which he dedicated to his servant untrained in mathematics. He is credited
for the development for a new branch of mathematics called Topology. On 18
September 1783 he died in St Petersburg in Russia.
3. Harshad Number:- A
number is called Harshad Number if it is divisible by the sum of its digits.
1729 is a Harshad number as it is divisible by the sum of its digits 1 +7 + 2 +
9 = 19. The word Harshad has its origin from the Sanskrit language and it means
great joy. Harshad Numbers were defined by the Indian mathematician D.R.Kaprekar.
It is also known as Niven numbers in the name of mathematician Ivan M. Niven.
4.. Kaprekar Number:- 6174 is called Kaprekar number.
Here is the method to find a Kaprekar Number:-
Take any four digit number whose all digits
are not equal. Arrange this number in descending order and then reverse it. Subtract
these two. Repeat the process after few steps once or a while you shall find
6174.
|
Take a
number 1234
Arrange in
descending order 4321
Reverse it 1234
---------------------------------------- ----------
Subtract it 3087
Arrange in
descending order 8730
Reverse it 0378
---------------------------------------- ---------
Subtract it 8352
Arrange in
descending order 8532
Reverse it 2358
---------------------------------------- ----------
Subtract it 6174(Kaprekar
constant)
Moreover, there
is another form of Kaprekar number. A number is said to be Kaprekar number if
for a given base the sum of square of the two split part of the number gives
back the original number. Example :- 99 is
a Kaprekar number 992
= 9801 and 98 + 01 = 99
The first ten
Kaprekar numbers are -1, 9, 45, 55, 99, 297, 703, 999,2223 and 2728
5. Fermat Number: - Numbers of the type Fn =
for
n =1, 2, 3… are called Fermat Numbers. Piere De Fermat wrote to Mersenne on
December 25, 1640 that:
If I can determine the basic reason why 3,
5, 17, 257, 65537... are prime numbers, I feel that I would find very
interesting results, for I have already found marvelous things(along these
lines) which I will tell you about later.
Fermat thought that these numbers might be
primes but it is not true for F5. In 1732 Euler discovered that F5 is divisible
by 641.
F5 = 641 x 6700417 =4294967297
|
.
6. Fibonacci Number: - 1, 1, 2, 3, 5, 8, 13… are the Fibonacci
numbers. It is the set of numbers which after the second is the sum of the two
previous ones.1+1=2, 1+2=3, 2+3 =5 and so on. The definition of the Fibonacci
series is:-
Fn+1 =
Fn-1 + Fn, if
n> 1
F0 = 0 and F1
= 1
|
Fibonacci numbers can be generated with the
help of the Pascal’s triangle.
In general the Pascal’s triangle is written
as
|
Now in order to find the Fibonacci numbers
from it arrange its digits so that 1’s in the left hand are below each other as
shown in the figure below. Fibonacci numbers can be obtained by summing up the
arrowed numbers as shown here.
7.
Liouville Number Any number of the form
where A is a constant, is called a Liouville
Number
|
.
8. Pythagorean Numbers:- Any set of positive integers satisfying the
equation
x2
+ y2 = z2
is
called Pythagorean numbers. Such numbers are given by
m2- n2 , 2mn, m2 + n2 where m and n are arbitrary positive
integers with the condition that m ≠n . More over n, ½(n2-1) and ½(n2-1)
+1 are also the set of Pythagorean
triplets.
( 3,4,5), (5,12,13), (6,8,10),
(7,24,25),(8,15,17),(9,40,41),(11,60,61)… are the example of Pythagorean
numbers.
|
9. Markov
Number: - It is a positive integer x, y, z that is the part of the solution
of the equation
The first ten
Markov numbers are – 1, 2, 5, 13, 29, 34, 89, 169, 233 and 433. It was
discovered by Andrey Markov.
10. Smith Number: It is a composite number.
For a given base, the sum of its digits is equal to the sum of the digits in
its prime factorization. Example:
- 22 is a smith number because it has two prime factors 2 and 11 and the sum of
22 is equal to the sum of digits of its prime factors 2 and 11-- 2 + 2 = 2 + 1 + 1
This number is
named after Harold Smith and was studied by Albert Wilansky of Lehigh University.
Albert notices this property in the phone number of his brother in law Harold
and dedicated such number by giving his name. The phone number of Harold smith
was 4937775. The prime factorization of 493775 is 3, 5, 5, and 65837. 4937775 =
3 × 5 × 5 × 65837 and 4 + 9 + 3 + 7 + 7 + 7 + 5 =
3 + 5 + 5 + 6 + 5 + 8 + 3 + 7 =
42.
The first ten
Smith numbers are -- 4, 22, 27, 58, 85, 94, 121, 166, 202 and 265.
11. Sohie Germain Prime numbers: - It is a
prime number. For a given prime p, if 2p + 1 is also a prime it is called
Sophie Germain Prime. It is named after
French mathematician Marie Sophie Germain. The first few such numbers are –2 ,
3, 5, 11, 23 ,29, 41..
12. Lucas Numbers:- A series of numbers
2, 1, 3, 4, 7, 11,
18, 29, 47, 76, 123, 199, 322, 521…
is called Lucas numbers
Ln = Ln-1 + Ln-2
for
n>1 is called Lucas series where L0 = 2 and L1 = 1.
|
13. Mersenne Numbers:-Numbers in the form of Mn
= 2p – 1 are called Mersenne Numbers. In 1644 Mersenne
claimed that if p = 2, 3 , 5, 7, 13, 17,
19, 31, 67, 127, and 257 ; Mn is prime
and for all the other n<257 Mn is composite.
This conjecture was proved wrong over the years.
|
14. Wison Prime:- If p is a prime such that
p2 divides (p – 1 )! + 1 it is called Wilson number, where ! denotes
the factorial of a number. It is named after English mathematician John Wilson
(1741 – 1793). The only known Wilson primes are 5, 13 and 563
There are many
such number which is not addressed here due to some limitation and I do hope
that the readers after enjoying such numbers will take initiative to find out
such numbers themselves.
Rush your comments to
Rajesh kumar Thakur
rkthakur1974@gmail.com
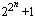







No comments:
Post a Comment