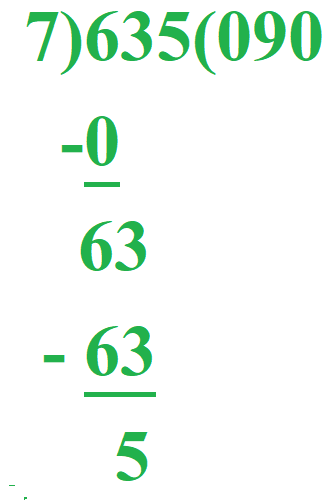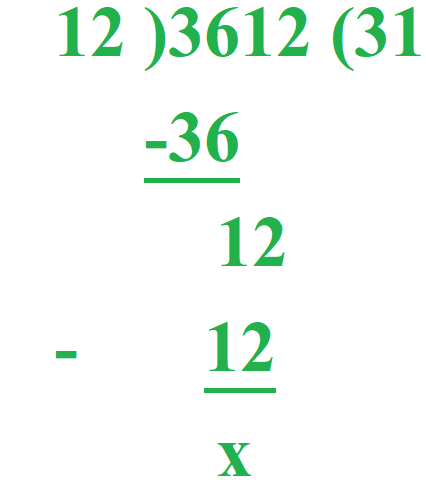INDIAN KNOWLEDGE SYSTEM -LECTURE AT G D GOENKA PUBLIC SCHOOL SILIGURI

 

Women Mathematicians from India ---- K Bhanumoorthy

 

CONTRIBUTION BY WOMEN IN MATHEMATICS

A quote from Marie Curie, Noble prize winner & Radio Activity researcher

“We must have perseverance and above all confidence in ourselves. We must believe that we are gifted for something and that this thing ,at whatever   cost ,must be attained.”

Introduction:

I was given an opportunity to write an article on “The Importance of Women Education in the Society”, got published on the title of the book “Women Empowerment and Educational development”. Very recently people celebrated International Women’s Day on March 8^th. Some organisations recognised the immense services rendered by women on various fields, had been felicitated with awards and rewards. Since then, I have been thinking to write an article on the topic given above. There is an assumption that girls can’t do maths. How can one accept this statement? The assumption is wrong, if I am permitted to say. Here are the five women Mathematicians from our country:

1.       Ms. Shakuntala Devi

2.       Ms. Raman Parimala

3.       Dr. Mangala Narlikar

4.       Ms. Sujatha Ramdorai

5.       Dr. Neena Gupta

There are past and present exceptional women mathematicians, let me share what they have contributed.

1.      Shakuntala Devi: She was born on November 4^th, 1929 in Bangalore, Karnataka. She redefined women can rule the domain of maths. She is called as Human Computer. She extracted 23^rd root of two hundred- and one-digit number in 50 seconds. This has been published and listed in Guinness book of world records in 1980. She has been very popular on mental calculations. She has also written books, to name few: Puzzles to Puzzle You, Super memory, etc. She has also touched little bit of the theory of astrology.

 

                                               

2.     Raman Parimala: She was born on November 21^st, 1948. During those days, women were not allowed to work on mathematics. Yet, she took up. She has been expertise in Algebra, Algebraic Geometry, Topology. She was felicitated the highest science award in India, Shanti Swarup Bhatnagar price in 1987. She enjoyed teaching students, encouraged especially women to pursue Study in Mathematics. Her services have been recognised under the fellow of The Indian National Science Academy. She also worked at TIFR, Mumbai. She worked as Maths professor in Emory University.

                                          

3.       Dr. Mangala Narlikar: She was born on 1^st January, 1946 in Mumbai. She used to hear maths is a male dominated subject, girls are bad at maths/calculation. She never believed, in fact, refused to believe as she stood top in every exam both in BA and MA in maths. She has been a mathematics wizard, used to count stars. Her family members supported her academic career, so she pursued her PhD in Mathematics and worked in colleges as lecturer. She has written papers on Maths. She is specialised in Pure Mathematics. She made even difficult problems easier by her simple easy approach. She taught girls in slum area. She worked as a Chairman of Bal Bharti. She says “if you want to learn universal ethics and norms, mathematics is a brilliant teacher”.

 

4.       Ms. Sujatha Ramdorai: She was born in the year 1962 in Bangalore. She is the first and the only Indian to win ICTP (International Centre for Theoretical Physics) Ramanujan Prize in 2006, and also Shanti Swaroop Bhatnagar Award in 2004. She is working in TIFR as a professor in Maths. She is also member of the scientific committee of several international research centres; Indo-French centre for Promotion of Advance Research. She is specialised in pure and applied maths. She worked in the field of arithmetic geometry of elliptic curves. She said Scientific career helps women to carry out family life with flexibility, and also said one can achieve excellence by just understanding Maths.

  

5.       Dr. Neena Gupta: She was born in the year 1984 in Kolkata. She is an associate professor at the theoretical statistics and mathematics unit of Indian Statistical Institute (ISI, Kolkata). She is the youngest to receive Shanti Swaroop Bhatnagar Award in 2019. She has been recognised for her work in Affine Algebraic Geometry and for suggesting a solution for the ZARISKI cancellation problem which mathematicians from 20^th and 21^st centuries have been trying to solve. She got published her first research paper on the mathematics puzzle ZARISKI cancellation during the year 2014. She received the award from Indian National Science Academy also. Her field of research is mainly on commutative algebra and affine.

                                                

Conclusion:

I feel happy that I could be aware of eminent people who have contributed in mathematics. No doubt, many more are there though I have listed only five in numbers. Let me continue who have contributed from the other countries in the field of mathematics.

  “Mathematics is the Music of Reason.” --- James Joseph Sylvester (An English Mathematician).

 

                                                                                                               ---- be continued

Compiled by :- Mr K Bhanumoorthy (Rtd Principal, KVS)

How 7)635( works?

 Division is a continued subtraction process. 

12 / 4 is basically getting the remainder 0 or less than 3 after repeated subtraction.

12 - 4 = 8 (1st step)

8 - 4 = 4 (2nd step)

4 - 4 = 0 (3rd step)

In order to get the result quickly, we multiply the divisor with a number that gets us closer to dividend. Ex :- 7)635(

Since subtracting 7 repeatedly from 635 will take long time so we reduce this process of subtracting a number by choosing a number by which 7 should be multiplied to get a number closer to 635.

Now look at the question.

In the second step, after subtraction when a digit (5)  carried down  is less than the divisor (7), we need to place a zero in the quotient.

This can be understood in other ways. If we don't restrict a child to multiply a divisor by a number in between 1 to 9, such mistake can be avoided. Let's allow a child to choose a number by which 7 is multiplies so as to reach around 635 then the child will obviously multiply 7 by 90 to reach 630

In many countries, if the first digit of dividend is less than divisor, the first digit of the quotient is taken as zero. In simple terms, we begin with zero as the first digit of quotient in such case.

Take another example to understand the mystery of ZERO.

Example :- 

When you are carrying down one digit from the dividend and that digit is less than the divisor as shown in the above case, you need to place a zero in the quotient. It can be understood in simple terms that, if you are left with another digit in the dividend and the carry down digit is not big enough to be divided by divisor, then placing an extra zero in the quotient, allows you to carry down the second digit.

How algorithm to find the Square Root of a number work?

 Question:- How algorithm to find the square root of a number works?

Answer:- Square of a number is multiplying a number by itself. Finding the square root of a number is to obtain one factor out of two.

5 x 5 = 25 is called squiring a number.

Square root of 25 is  obtained by finding a pair of prime factor and selecting one.

The square root of a number, N, is the number, M, so that M² = N. The square root algorithm is set up so that we take the square root of a number in the form of (X + R)². The square root of this number is obviously (X + R). X represents the current approximation for the square root, and R represents the remainder of the number left over from the approximation. Our approximation will always be the correct square root of the number truncated (not rounded) to the number of digits in our approximation. If we expand our number (X + R)² it will equal X² + 2RX + R². This gives us the basis for our derivation of the square root algorithm.

Step 1: The square root of a number between 1 and 100 is a number between 1 and 10. 

Step 2: Grouping of a  number is done from right to left in pair. The number of groups determine the number of digits a square root of number have.

Step 3: Suppose a perfect square root is in the form of  X² + 2RX + R². 

We subtract off the current approximation, X², which gives 2RX + R²

Step 4: 2RX + R² = R(2X + R). 

Here our current approximation, X, is doubled resulting in 2X, which are the first digits of the number we will be working with.

Step 5: The correct approximation of R will determine the two digits of the square root. This number (R) must divide into the next grouping with the smallest remainder.

Step 6: The procedure can be repeated as many times as necessary until either no remainder is found.

Example:-